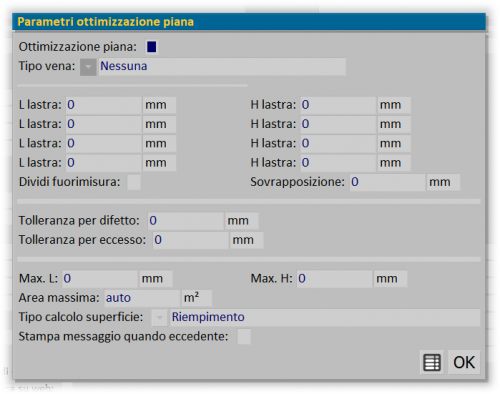
Parametri ottimizzazione piana
Da Opera Wiki.
Versione delle 10:51, 26 ott 2023, autore: Monica.Sanna (Discussione | contributi)
Indice |
Lo scopo di questo archivio è quello di gestire i limiti dimensionali del riempimento e i messaggi nelle stampe. Consente anche di gestire l'Ottimizzazione piana integrata, se viene attivato il relativo step.
I campi per l'ottimizzazione piana integrata
- Ottimizzazione piana (step opzionale): se attiva, esegue l'ottimizzazione per questo riempimento sulla base delle dimensioni impostate nei campi seguenti.
- Tipo vena
 : campo per la scelta del tipo di vena del riempimento (Nessuno, Vena orizzontale, Vena verticale) ed è legato alla gestione del taglio della lastra.
: campo per la scelta del tipo di vena del riempimento (Nessuno, Vena orizzontale, Vena verticale) ed è legato alla gestione del taglio della lastra.
- L lastra/H lastra: larghezza e altezza del riempimento da ottimizzare.
- Dividi fuorimisura: divide i tagli oltre la misura del foglio. L'Ottimizzazione piana eseguita sulla base delle dimensioni della lastra impostate nei campi Llastra e H lastra viene calcolata in pezzi. le parti della lastra che eccedono le misure impostate vengono divise e calcolate in m2.
- Sovrapposizione: campo per impostare la misura di sovrapposizione dei pezzi divisi.
I campi per la gestione dei messaggi e delle dimensioni dei riempimenti
- Tolleranza per difetto/Tolleranza per eccesso: in questo campo definiamo la tolleranza nell'arrotondamento (per difetto o per eccesso) delle dimensioni del riempimento. I campi sono utili nel dimensionamento dei riempimenti su infissi con più strutture ( per es. una vetrata) che per loro progettazione sono composte da strutture diverse tra loro per dimensioni. Indicare la tolleranza per i riempimenti consente di dimensionarli tutti alla stessa misura.
- Max. L/Max. H: dimensioni massime del riempimento.
- Area massima: superficie per il calcolo delle inglesine.
- Tipo calcolo superficie
 : indica quale superficie viene presa in considerazione per il calcolo (Riempimento, Superficie in vista)
: indica quale superficie viene presa in considerazione per il calcolo (Riempimento, Superficie in vista)
- Stampa messaggio quando eccedente: se attivo, stampa un messaggio di errore quando il riempimento eccede le dimensioni massime.